আইওটি ডিভাইস সহ আধুনিক প্রযুক্তিতে লজিক গেট (Logic Gates) এর ভূমিকা অনেক। এক আর এক যোগ করলে কত হবে? প্রশ্নটি খুবই শিগ্রই সলভ হয়ে গেল, তাই তো? কিন্তু আপনি একবার চিন্তা করুন, একার ১ যোগ করলে যে ২ হবে তা আপনি কিভাবে বুঝতে পারেন? উত্তর খুবই সিম্পল—মস্তিষ্কের মাধ্যমে। আমাদের মস্তিষ্ক এমনভাবে তৈরি, যা শর্তভিত্তিক বিষয় সমাধান করতে সক্ষম। একার একের ক্ষেত্রে শর্ত ছিল যোগ, এবং এ শর্ত অনুযায়ী এক আর এক একসাথে করে মস্তিষ্ক সমাধানে পৌঁছে।
কিন্তু কম্পিউটারের তো কোনো মস্তিষ্ক নেই। কম্পিউটার জাস্ট কিছু প্রাণহীন যন্ত্রাংশ দিয়ে তৈরি। তাহলে কম্পিউটার কিভাবে মানুষের চেয়ে হাজার গুণ দ্রুত তার সাথে ম্যাথমেটিক্যাল প্রবলেম সলভ করে?
কম্পিউটার বাদ দিন, জাস্ট নরমাল ক্যালকুলেটরই এমন সব ক্যালকুলেশন মুহূর্তেই করে ফেলে যা মানুষের মস্তিষ্কের মাধ্যমে করতে গেলে দীর্ঘ সময়ের প্রয়োজন। তাহলে এখন প্রশ্ন হচ্ছে, কম্পিউটারে এমন কী বিষয় রয়েছে যা শর্তভিত্তিক বিষয়গুলোকে মুহূর্তে সমাধান করতে সক্ষম? এর উত্তর হচ্ছে লজিক গেট।
আজকের ভিডিওতে এই লজিক গেট সম্পর্কে বলা হবে। আমি জুম্মান আছি আপনাদের সাথে। আপনারা দেখছেন বিজ্ঞান পাইসি।
লজিক গেট সার্কিট (Logic gate circuit AND, OR, NOT)

এটি খুবই সিম্পল একটি সার্কিট হলেও এখানে কী ঘটবে তা বুঝতে পারলে আপনি লজিক গেট তথা কম্পিউটার কিভাবে ম্যাথ প্রবলেম সলভ করে তা বুঝতে পারবেন। এখানে একটি ব্যাটারির সাথে একটি বাতি সংযুক্ত রয়েছে। সেই সাথে দুইটি সুইচ এ এবং বি রয়েছে। এখন যদি এ সুইচ অন থাকে কিন্তু বি সুইচ অফ থাকে তাহলে কি বাতি জ্বলবে? উত্তর হচ্ছে না, কারণ এমন ক্ষেত্রে বাতিতে বিদ্যুৎ পৌঁছবে না। একমাত্র দুইটি সুইচ যদি অন থাকে তবেই বাতি জ্বলবে।
এবার এটি আপনি খেয়াল করুন। এখানে একমাত্র দুইটি সুইচ যদি অফ থাকে তবেই কেবল বাতি জ্বলবে না। অন্য সকল ক্ষেত্রে বাতি জ্বলবে। অর্থাৎ দুইটি সুইচ যদি অন থাকে তবে বাতি জ্বলবে। আবার যদি দুইটির যেকোনো একটি অন থাকে, সেক্ষেত্রেও বাতি জ্বলবে। এবার এই সেটআপটি লক্ষ্য করুন। এখানে একটি মাত্র সুইচ রয়েছে।
আরও পড়ুনঃ ষাণ্মাসিক সামষ্টিক মূল্যায়ন ২০২৪ (সংশোধিত): ৬ষ্ঠ থেকে ৯ম শ্রেণি রুটিন
এখানে কিন্তু প্রচলিত ধারণার উল্টো ঘটনা ঘটবে। অর্থাৎ সুইচ অন করা হলে বাতি জ্বলার বিপরীতে নিভে যাবে। কারণ সুইচ অন করলে কারেন্ট পাস হবার জন্য শর্টকাট পথ হবে এই বরাবর। ফলে কারেন্ট বাতিতে আর পৌঁছবে না, যার কারণে সুইচ অন করলে বাতি নিভে যাবে এবং সুইচ অফ করলে বাতি জ্বলে থাকবে।
এখন এই যে তিনটি ভিন্ন সেটআপ দেখলেন, এগুলো যদি আপনি বুঝে থাকেন তবে আপনি লজিক গেট বুঝে গিয়েছেন। সেটা কিভাবে তা বলা যাক। এই সেটআপগুলোর ক্ষেত্রে সুইচ অন-অফ হচ্ছে ইনপুট এবং বাতি জ্বলা কিংবা না জ্বলা হচ্ছে আউটপুট। এখন আমরা জানি বিদ্যুৎ প্রবাহ থাকাকে অন কিংবা বাইনারিতে ১ বলা হয়। আবার বিদ্যুৎ প্রবাহ না থাকাকে অফ কিংবা বাইনারিতে ০ বলা হয়।
তাহলে প্রথম সেটআপে যা যা ঘটতে পারে তা যদি আমরা বাইনারিতে প্রকাশ করি তবে আমরা এই চারটি পাবো, যাকে বলা হয় ট্রুথ টেবিল। সেই সাথে এই সেটআপ আঁকা যেহেতু সময় সাপেক্ষ বিষয়, সেও তো এটিকে সংক্ষেপে এই সিম্বলের মাধ্যমে প্রকাশ করা হয় এবং একে বলা হয় এন্ড গেট। দ্বিতীয় সেটআপকে বলা হয় অর গেট, যাকে এই সিম্বলের মাধ্যমে প্রকাশ করা হয় এবং এর ট্রুথ টেবিল হচ্ছে এটি। তৃতীয় সেটআপকে বলা হয় নট গেট, যাকে প্রকাশ করা হয় এই সিম্বলের মাধ্যমে এবং ট্রুথ টেবিল হচ্ছে এটি।
এই তিনটি বেসিক লজিক গেট ছাড়াও আরও চারটি বেসিক লজিক গেট রয়েছে, যেগুলোকে প্রথমে উল্লেখ করা এই তিনটি লজিক গেটের মাধ্যমেই তৈরি করা হয়।
দশমিক ও বাইনারি সংখ্যা পদ্ধতি Decimal and Binary number system
এখন এই সকল লজিক গেট কিভাবে যোগ, বিয়োগ কিংবা অন্যান্য ক্যালকুলেশন করে থাকে তা বলার আগে বাইনারি এবং দশমিক সংখ্যা পদ্ধতি সম্পর্কে সামান্য কথা বলে নেওয়া দরকার।
দশমিক পদ্ধতিতে মোট অংক সংখ্যা দশটি—০ থেকে ৯ পর্যন্ত। যার ফলে ৯-এর পর আমাদেরকে আবার আগের অংকগুলোকে পুনরাবৃত্তি করতে হয়। ১০, ১১, ১২ ইত্যাদি। অন্যদিকে বাইনারি পদ্ধতিতে অংক সংখ্যা দুইটি—০ এবং ১।
যার ফলে ১-এর পরেই আবার আগের অংককে পুনরাবৃত্তি করতে হয়। অর্থাৎ দশমিক পদ্ধতির ২-কে বাইনারিতে প্রকাশ করার ক্ষেত্রে ১০ লিখতে হবে। ৩-এর ক্ষেত্রে হবে ১১। ৪-এর ক্ষেত্রে ১০০। ৫-এর ক্ষেত্রে ১০১। এভাবে চলতে থাকবে।
আরও পড়ুনঃ বন্যা কেন হয় এবং কোন বন্যা সবচেয়ে বেশি ভয়ংকর All kinds of Flood
লজিক গেট কিভাবে কাজ করে? How logic gates do math?
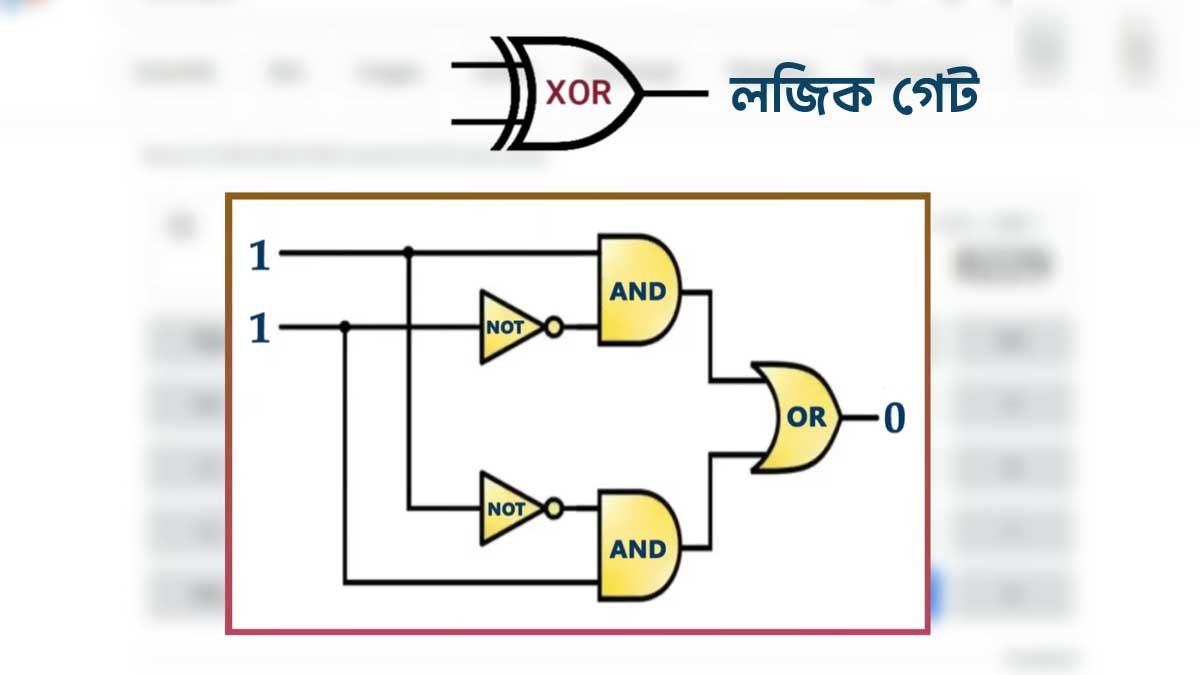
এবার কম্পিউটার কিভাবে যোগ করে এই বিষয়টি বলা যাক। এর জন্য আমাদের দুইটি লজিক গেট প্রয়োজন হবে। একটি হচ্ছে এক্সঅর এবং অন্যটি হচ্ছে এন্ড গেট। এখানে এক্সঅর গেট কিন্তু আবার পাঁচটি গেটের সমন্বয়ে তৈরি।
দুইটি নট গেট, দুইটি এন্ড গেট এবং একটি অর গেট। এখানে অবশ্যই বিষয়টি বিস্তারিত বলছি না। তবে এটুকু বলি, এক্সঅর গেটের দুটি সুইচের যেকোনো একটিকে অন রাখলেই কেবল আউটপুট ১ আসবে।
এবার এক্সঅর এবং এন্ড গেটের মাধ্যমে একদম সাধারণ একটি যোগ করা যাক, এবং তা হচ্ছে ১ + ১। এই সার্কিটগুলোর ক্ষেত্রে একটি বিষয় খেয়াল করুন। এখানে জাস্ট ২ বিটের ইনপুট সুযোগ রয়েছে এবং আউটপুটও সর্বোচ্চ ২ বিটের পাওয়া যাবে। এখন বোঝার সুবিধার জন্য সেটআপটিকে ঘুরিয়ে নেওয়া যাক। এখানে আমাদের ইনপুট হচ্ছে ১ এবং ১। অর্থাৎ ইনপুট অংশের দুইটি সুইচই ১ থাকবে।
এখন এই ১, ১ ইনপুটের ক্ষেত্রে এক্সঅরের লজিক অনুযায়ী আমরা আউটপুট পাবো ০। অর্থাৎ এক্সঅর গেটের আউটপুটে থাকা লাইটটি অফ থাকবে। অন্যদিকে একই ইনপুট দিয়ে যাবার ক্ষেত্রে লজিক অনুযায়ী আউটপুট হবে ১। অর্থাৎ এন্ড গেটের বাতি জ্বলবে।
তাহলে এখানে খেয়াল করুন, ওয়ান এবং ওয়ান ইনপুট দেয়ার ফলে আমরা আউটপুট পেয়েছি ওয়ান জিরো। এখন এই ওয়ান জিরো বাইনারি সংখ্যাটিকে দশমিক পদ্ধতিতে কনভার্ট করলে আমরা পাবো টু। তার মানে আমরা এই সেটআপের মাধ্যমে ওয়ান এবং ওয়ান যোগ করতে সক্ষম হয়েছি।
এখন প্রশ্ন হচ্ছে, বড় সংখ্যার যোগ কি এই সেটআপের মাধ্যমে করা যাবে? উত্তর হচ্ছে না, কারণ এই সেটআপের ক্ষেত্রে আমরা সর্বোচ্চ দুই বিটের আউটপুট পাবো। এর চেয়ে বেশি বিটের রেজাল্ট পেতে হলে আমাদেরকে গেট সংখ্যা বাড়াতে হবে। এখানে যে সেটআপটি দেখেছেন, একে বলা হয় হাফ অ্যাডার। এরকম দুটি হাফ অ্যাডার একসাথে যুক্ত করলে তাকে বলা হয় ফুল অ্যাডার বা শুধু অ্যাডার।
এই ফুল অ্যাডারের অরগেট থেকে আসা আউটপুটটি যোগ করার ক্ষেত্রে হাতে থাকা যে বিষয়টি থাকে, তার কাজ করে। ফলে অরগেটের আউটপুট পরবর্তী ফুল অ্যাডারের দ্বিতীয় এক্সোর গেটের সাথে যুক্ত থাকে। এখন আপনি যত বেশি ফুল অ্যাডার পরস্পরের সাথে যুক্ত করবেন, তত বেশি বিটের সংখ্যা যোগ করতে পারবেন। যেমন এখানে ছয়টি ফুল অ্যাডার পরস্পরের সাথে যুক্ত রয়েছে, যার ফলে আউটপুটে বাতি রয়েছে ছয়টি। তার মানে এখান থেকে আমরা সর্বোচ্চ ৬ বিটের বাইনারি সংখ্যা পর্যন্ত রেজাল্ট পাবো।
আরও পড়ুনঃ জেট ইঞ্জিন কি এবং কিভাবে কাজ করে Jet engine explained in Bangla
এখন মনে করুন, এই সেটআপের মাধ্যমে আমরা ১৫+১২ যোগ করব। ১৫ এর বাইনারি হচ্ছে ওয়ান ওয়ান ওয়ান ওয়ান এবং ১২ এর বাইনারি হচ্ছে ওয়ান ওয়ান জিরো জিরো। এখন একদম ডানদিকের দুইটি ডিজিট অর্থাৎ ওয়ান জিরো ইনপুটের ক্ষেত্রে, প্রথম অ্যাডারের প্রথম এক্সোর থেকে আসবে ওয়ান। পরবর্তীতে এই ওয়ান দ্বিতীয় এক্সোরে যাবে।
সেখানে অন্য একটি ইনপুট হবে জিরো, কারণ একদম প্রথমে হাতে কিছু নেই, অর্থাৎ ওই ইনপুটের স্থানে কোনো সিগন্যাল নেই। সুতরাং, ওয়ান এবং জিরোর ইনপুটের জন্য দ্বিতীয় এক্সোরের মাধ্যমে ফাইনাল রেজাল্ট পাবো ওয়ান, যার ফলে প্রথম অ্যাডারের বাতিটি জ্বলে থাকবে।
অন্যদিকে, নিচের দুইটি এন্ড এবং একটি অরগেট থেকে রেজাল্ট পাবো জিরো, যা হাতে থাকবে। অর্থাৎ, পরবর্তী ফুল অ্যাডারের দ্বিতীয় এক্সোরের সাথে যুক্ত থাকবে। পরবর্তী ওয়ান জিরো ইনপুট দ্বিতীয় অ্যাডারের প্রথম এক্সোরে যাবে, যা থেকে আউটপুট পাবো ওয়ান। অন্যদিকে, প্রথম অ্যাডারের আউটপুট আসবে জিরো। ফলে দ্বিতীয় অ্যাডার থেকে ফাইনাল রেজাল্ট পাবো ওয়ান এবং হাতে থাকবে জিরো।
তারপরবর্তী ওয়ান ওয়ান ইনপুটের জন্য তৃতীয় অ্যাডারের প্রথম এক্সোর থেকে আউটপুট পাবো জিরো। এর আগের অ্যাডার থেকে আসা ইনপুট হবে জিরো। অর্থাৎ, তৃতীয় অ্যাডারের দ্বিতীয় এক্সোরে জিরো এবং জিরো ইনপুট হবে।
এর জন্য ফাইনালি আমরা রেজাল্ট পাবো জিরো। অর্থাৎ, তৃতীয় অ্যাডারের বাতি জ্বলবে না। সেই সাথে অরগেটের আউটপুট হবে, যা চতুর্থ অ্যাডারের দ্বিতীয় এক্সোরের সাথে যুক্ত রয়েছে।
সর্বশেষ ওয়ান ওয়ান ইনপুটের জন্য চতুর্থ অ্যাডারের প্রথম এক্সোর থেকে পাবো জিরো। যা আগের অ্যাডার থেকে আসা ওয়ানকে নিয়ে দ্বিতীয় এক্সোরে প্রবেশ করবে এবং ফাইনাল রেজাল্ট পাবো ওয়ান। অর্থাৎ, চতুর্থ অ্যাডারের বাতি জ্বলে থাকবে এবং অরগেটের আউটপুট হবে ওয়ান।
এখনই সর্বশেষ অরগেট থেকে আসা ওয়ান পঞ্চম অ্যাডারে প্রবেশ করবে এবং ফাইনাল রেজাল্ট শো করবে ওয়ান, যার ফলে পঞ্চম অ্যাডারের বাতি জ্বলে থাকবে। তাহলে আমাদের ফাইনাল রেজাল্ট হচ্ছে ওয়ান ওয়ান জিরো ওয়ান ওয়ান। যাকে দশমিক পদ্ধতিতে কনভার্ট করলে হবে ২৭। সুতরাং, আমরা এই সার্কিটগুলোর মাধ্যমে ১৫+১২ যোগ করতে সক্ষম হয়েছি।
এভাবে এখানে যত অ্যাডার যুক্ত করা হবে, ততই বড় বড় সংখ্যা যোগ করা যাবে। বিয়োগ করার ক্ষেত্রে লজিক গেটের সেটআপ হবে এমন। আবার গুণ করার ক্ষেত্রে এমন।
এখনই বেসিক ম্যাথমেটিকসগুলো বাদ দিয়ে যদি আমরা আরও হাই লেভেলের কমপ্লেক্স ম্যাথ সমাধান করতে চাই, সে ক্ষেত্রে লজিক গেটের কম্বিনেশন হয়ে উঠবে আরও কমপ্লেক্স। বর্তমান সময়ে কোটি কোটি লজিক গেট বিভিন্ন কম্পিউটিং সার্কিটে ব্যবহৃত হয়।
সাধারণ ক্যালকুলেটরের জটিল ক্যালকুলেশন যেমন সাইন, কসাইন ইত্যাদির জন্য উপযোগী লজিক গেটের সমন্বয় থাকে না। ফলে সাধারণ ক্যালকুলেটর শুধু যোগ, বিয়োগ, গুণ, ভাগ এগুলো করতে পারে।
অন্যদিকে, সায়েন্টিফিক ক্যালকুলেটর কিংবা কম্পিউটার যেকোনো কমপ্লেক্স প্রবলেম সমাধান করতে পারে, কারণ সেখানে সেই অনুযায়ী লজিক গেটের সমন্বয় থাকে।
এখন প্রশ্ন হচ্ছে, কম্পিউটার কিভাবে বোঝে যে কখন তাকে যোগ করতে হবে কিংবা কখন একটি ভিডিও প্লে করতে হবে? এর পেছনে রয়েছে সফটওয়্যার। এই সফটওয়্যারের জন্য প্রয়োজন কোডিং। কোডিং হচ্ছে মানুষের বোধগম্য করে তৈরি করা কম্পিউটার ল্যাঙ্গুয়েজ, যার মাধ্যমে কম্পিউটারকে নির্দেশ দেয়া যায় কখন কী করতে হবে।
আপনি যত সফটওয়্যার আপনার মোবাইল কিংবা কম্পিউটারে দেখেন, সব কিছুই কিন্তু কোডিং এর মাধ্যমে প্রোগ্রাম করা হয়েছে। ব্রাউজ করার সময় যে ওয়েব পেজগুলো দেখেন, এগুলো কোডিং এর মাধ্যমে তৈরি। তাছাড়া বর্তমানে এই আইটি নিয়ে যে এত আলোচনা, এর পেছনেও রয়েছে কোডিং।
আরও পড়ুনঃ মিটার নির্ণয় ইতিহাস Meter History and Meter Definition
Logic gate switch history (Relay, Vacuum tube, Transistor)
হাফ অ্যাডারের মাধ্যমে জাস্ট ২ বিটের যোগফল বের করার জন্যই মোট সুইচ প্রয়োজন দশটি। এখন আপনার মনে প্রশ্ন আসতে পারে, ফিজিক্যালি যদি সুইচ ব্যবহার করা হয় তবে তো একটি সাধারণ ক্যালকুলেটরের আকার হবে বিশাল। সেখানে বর্তমানে পাওয়ারফুল কম্পিউটারগুলোর প্রসেসর এত ছোট থাকে কিভাবে?
১৯৩৭ সালে ক্লড শ্যানন তার থিসিস লিখতে গিয়ে বলিয়ান অ্যালজেব্রার সাথে ইলেকট্রিক্যাল সার্কিটের সম্পর্ক লক্ষ্য করেন। ওই বছরে জর্জ স্টিবিটজ সর্বপ্রথম ডিজিটাল ক্যালকুলেটর তৈরি করেন, যা মডেল কে নামে পরিচিত। এর আগে যত গণনাযন্ত্র ছিল, তার সবগুলোই ছিল এনালগ।
জর্জেটিভিজের ক্যালকুলেটর মূলত ছিল প্রথমে উল্লেখ করা ওয়ান এবং ওয়ানে যোগফল করার ক্ষেত্রে যে লজিক গেট প্রয়োজন ছিল, সেই লজিক গেটের সমন্বয়। স্টিবিস্তার যন্ত্রে সুইচের স্থলে ব্যবহার করেন ইলেকট্রিক্যাল রিলে।
যেখানে একটি ইলেকট্রনিক্স থাকে এবং ইলেকট্রনিক্সে তরিত প্রভাব দিলে তা চুম্বকে পরিণত হয়, যা তার পাশে থাকা ম্যাটারকে আকর্ষণ করে। এর মাধ্যমে তরিত ব্যাড সুইচ অফ কিংবা অন করা যায়।
যেমন মনে করুন, তিনটি অ্যান্ড গেট পরস্পরের সাথে এইভাবে যুক্ত রয়েছে। তার মানে এখানে এই চারটি সুইচ হচ্ছে ইনপুট, অর্থাৎ আপনি নিজ হাতে সুইচ অন-অফ করে ইনপুট দিবেন। কিন্তু ভেতরে থাকা এই দুইটি সুইচের তো আর হাতে ইনপুট দেওয়ার সুযোগ নেই, কারণ এই দুইটি সুইচ ইনপুটের অংশ নয়।
সুতরাং ভিতরের এই দুইটি সুইচ এমন হতে হবে যা ইনপুটের উপর ভিত্তি করে লজিক অনুযায়ী স্বয়ংক্রিয়ভাবে অন-অফ হবে। এবং এই জন্যই এই দুটি স্থানে সুইচ হিসেবে ব্যবহার করা হয় রিলে।
এখন মনে করুন, আপনি ইনপুটের চারটি সুইচ অন করে দিয়েছেন। তাহলে এই অ্যান্ড গেটের আউটপুট হবে ওয়ান। অর্থাৎ এই রিলেতে তরিত প্রভাব থাকবে, যার ফলে এই রিলের ইলেকট্রোম্যাগনেট সক্রিয় হবে।
এর প্রভাবে এই অ্যান্ড গেটের সুইচ স্বয়ংক্রিয়ভাবে অন হবে। অন্যদিকে এই অ্যান্ড গেটের ক্ষেত্রেও একই ঘটনা ঘটবে। এই সুইচ স্বয়ংক্রিয়ভাবে অন হবে, যার ফলে ফাইনাল আউটপুট হবে ওয়ান। অর্থাৎ আউটপুটের বাতি জ্বলবে।
জর্জেটিভিজের ডিজিটাল ক্যালকুলেটর তৈরির ২ বছর পর বেল ল্যাব চারশোটি রিলে ব্যবহার করে ৮ অঙ্কের দুটি দশমিক সংখ্যার ক্যালকুলেশন করতে সক্ষম এমন ক্যালকুলেটর তৈরি করে, যার নাম ছিল মডেল ওয়ান। সুইচ হিসেবে রিলে ব্যবহার করার ক্ষেত্রে মোটা দাগে তিনটি সমস্যা ছিল।
প্রথমত, এগুলোর সাইজে বড়। দ্বিতীয়ত, মুভিং পার্টস থাকার কারণে ক্যালকুলেশন করার সময় প্রচুর শব্দ তৈরি হতো। তৃতীয়ত, রিলের যেহেতু মোটামুটি ওজন ছিল, ফলে এগুলো মুভ করতে কিছুটা সময়ের প্রয়োজন ছিল। অর্থাৎ ক্যালকুলেশন করার ক্ষেত্রে ভালোই সময় লাগত।
আরও পড়ুনঃ সেকেন্ড নির্ণয় ইতিহাস Time keeping history and Second definition
যেমন হার্ভার্ড মার্ক ওয়ান সেকেন্ডে বড় সংখ্যার তিনটি যোগ কিংবা বিয়োগ করতে পারত। একটি গুণ করতে ৬ সেকেন্ড সময় নিতো এবং একটি ভাগ করার ক্ষেত্রে ১৫ সেকেন্ড সময় লাগতো। তাছাড়া কিছুটা জটিল ম্যাথ যেমন ত্রিকোণমিতির ফাংশন সমাধান করতে ১ মিনিটের চেয়েও বেশি সময় নিতো।
তার ওপর মুভিং পার্টস থাকার ফলে তা ভেঙে যেত কিংবা ক্ষয় হয়ে যেত। হার্ভার্ড মার্ক ওয়ানে ৩৫০০টি রিলে ব্যবহার করা হয়েছিল এবং গড়ে প্রতিদিন প্রায় ১৪০টি রিলে রিপ্লেস করা লাগতো। তাছাড়া এত বিশাল যন্ত্রের অন্ধকার এবং উষ্ণ পরিবেশ পোকামাকড়কে আকর্ষণ করত।
যেমন ১৯৪৭ সালের সেপ্টেম্বরে হার্ভার্ড মার্ক টুয়ের রিলেতে একটি মৃত মথ বা প্রজাপতি পাওয়া গিয়েছিল, যা মেশিনের সমস্যা তৈরি করেছিল। যার প্রেক্ষিতে গ্রেস হপার বলেছিলেন, কম্পিউটারে যদি কোনো সমস্যা দেখা দেয় তবে ধরে নিতে হবে মেশিনে পোকামাকড় বা বাগ রয়েছে।
এবং সেখান থেকেই আমরা বর্তমানের কম্পিউটার বাগস এই টার্মটি পেয়েছি। যাইহোক, রিলেতে বিভিন্ন অসুবিধা থাকার দরুন রিলের বিকল্প কিছু একটা প্রয়োজন পড়ে।
তখন সামনে আসে ভ্যাকুয়াম টিউব বা ট্রায়োড। ভ্যাকুয়াম টিউব মূলত ছিল বাতি, তবে সেখানে কিছু অতিরিক্ত বিষয় ছিল যার কারণে ভ্যাকুয়াম টিউব সুইচের মতো আচরণ করত। সাধারণত বাতিতে ফিলামেন্টের মধ্য দিয়ে ইলেকট্রন প্রবাহিত হয়, যা ফিলামেন্টের উত্তপ্ততার কারণে ফিলামেন্টকে উজ্জ্বল করে। ফলাফল হিসেবে ফিলামেন্ট থেকে আলো নির্গত হয়।
এখন এই সেটাপে আপনি একটি অতিরিক্ত তরিত প্রবাহ যোগ করুন। তারপর এ দুটি অংশের মাঝখানে আরেকটি তরিত প্রবাহ যোগ করুন। এখানে খেয়াল করুন, মাঝখানের অংশটিতে যদি পজিটিভ চার্জ অ্যাপ্লাই করা হয়, তবে ফিলামেন্ট থেকে ইলেকট্রন তৃতীয় অংশে যেতে পারবে, যা সার্কিটটিকে পূর্ণ করবে।
অর্থাৎ এই ক্ষেত্রে এটি সুইচ অন হিসেবে কাজ করবে। কিন্তু মাঝখানের অংশটিতে যদি নেগেটিভ চার্জ অ্যাপ্লাই করা হয়, তবে ফিলামেন্ট থেকে ইলেকট্রন শেষ প্রান্তে তৃতীয় পাত্রে যেতে পারবে না। ফলে সার্কিটটি পূর্ণ হবে না। অর্থাৎ এই অবস্থা সুইচ অফ হিসেবে কাজ করবে।
এই ভ্যাকুয়াম টিউবে রিলের মতো কোনো মুভিং পার্টস নেই। জাস্ট মাঝখানের অংশে পজিটিভ কিংবা নেগেটিভ চার্জ অ্যাপ্লাই করলেই তা সুইচ হিসেবে কাজ করে। ফলে পরবর্তীতে রিলের পরিবর্তে ভ্যাকুয়াম টিউব ব্যবহার শুরু হয়, যা রিলের তুলনায় বহুগুণ দ্রুত ক্যালকুলেশন করতে সক্ষম ছিল। তবে ভ্যাকুয়াম টিউবও কিন্তু পারফেক্ট ছিল না। প্রথমত, এটি ছিল খুবই ব্যয়বহুল। তাছাড়া এই ক্ষেত্রে প্রচুর পরিমাণ বিদ্যুতের প্রয়োজন পড়তো।
বড় স্কেলে প্রথম ভ্যাকুয়াম টিউব কম্পিউটার হচ্ছে ১৯৪৩ সালের কলসাস মার্ক ওয়ান, যাতে ১৬০০ ভ্যাকুয়াম টিউব ব্যবহার করা হয়েছিল। পরবর্তীতে ১৯৪৫ সালে তৈরি করা এনিয়াক সেকেন্ডে ৫০০০টি টেন-ডিজিটের দশমিক সংখ্যার যোগ কিংবা বিয়োগ করতে পারত, যা ছিল অতীতের যে কোনো কম্পিউটারের চেয়ে বহু বহুগুণ দ্রুতগতিসম্পন্ন। কিন্তু এর পরেও কম্পিউটারের জন্য ভ্যাকুয়াম টিউব পারফেক্ট সমাধান ছিল না।
আরও পড়ুনঃ শব্দ সমাচার What is sound, Sound wave properties and Anechoic room
যার ফলশ্রুতিতে পরবর্তীতে সামনে আসে সেমিকন্ডাক্টর-ভিত্তিক ট্রানজিস্টর, যা ডিজিটাল কম্পিউটেশনের ক্ষেত্রে আমূল পরিবর্তন নিয়ে আসে। কম্পিউটারকে পকেটে নিয়ে ঘোরার মতো সাইজে নিয়ে আসে। ট্রানজিস্টর কিভাবে সুইচ হিসেবে কাজ করে তা জানতে চাইলে এই ভিডিওটি দেখতে পারেন। ডেসক্রিপশন বক্সে লিংক পেয়ে যাবেন।
১৯৪৭ সালে বেল ল্যাব ট্রানজিস্টার জন্ম নেবার পরবর্তী সময়ে ট্রানজিস্টর ক্রমাগত ছোট হয়েছে।
বর্তমানে একটি ট্রানজিস্টারের সাইজ মাত্র কয়েকটি অ্যাটমের সমান। যার ফলে মোবাইল কিংবা কম্পিউটারের ছোট প্রসেসরে বিলিয়ন বিলিয়ন ট্রানজিস্টার বসানো সম্ভব হয়েছে, যা সেকেন্ডে কোটি কোটি জটিল সব ম্যাথমেটিক্স অপারেশন করতে পারে।
কম্পিউটার মূলত হচ্ছে গণনা যন্ত্র। এইজন্যই অতীত থেকে যত গণনা যন্ত্র আবিষ্কার হয়েছে, সবগুলি মূলত ছিল কম্পিউটার। এমনকি একসময় এমন কিছু কাজ ছিল, যেখানে মানুষ শুধুমাত্র বিভিন্ন ম্যাথ সলভ করত এবং তাদেরকে বলা হতো হিউম্যান কম্পিউটার।
বর্তমান সময়ে আমরা যে কম্পিউটার দেখি, এগুলো জাস্ট বিভিন্ন জটিল ম্যাথমেটিক্স অপারেশন করে, যার আউটপুট হিসেবে আমরা কম্পিউটারের যাবতীয় উপযোগিতা দেখে থাকি। এখন কম্পিউটার যে মানুষের চেয়ে বহুগুণ দ্রুত কোটি কোটি ক্যালকুলেশন করছে, এর পেছনের ব্রেইন হচ্ছে লজিক গেট।
পৃথিবীর স্বাভাবিক আবহাওয়াতে লক্ষণীয় পরিবর্তন দেখা যায় যখন এল নিনো কিংবা লা নিনার ঘটনা সংগঠিত হয়। এই এল নিনো কিংবা লা নিনার প্রভাবে হিটওয়েভ বা হিড্রোমের মতো ঘটনা ঘটে। এছাড়াও অতি বৃষ্টি, খরা, দাবানল তো রয়েছেই।
এল নিনো এবং লা নিনা সম্পর্কে বিস্তারিত জানতে এই ভিডিওটি দেখতে পারেন। ভিডিও ভালো লাগলে বিজ্ঞান পেইজের পরিবারের সাথে যুক্ত হয়ে সাথে থাকতে পারেন।















Comments ৩